Silindir, bir dikdörtgenin kenarlarından birinin etrafında döndürülmesiyle elde edilebilen silindirik geometrik bir cisimdir.
Silindirin yüzeyi şunlardan oluşur:
- Silindirin alt ve üst kısmında daire şeklinde iki özdeş yüzey.
- Karşıt taraflarından ikisinin çakışacağı şekilde ideal bir daire boyunca bükülmüş dikdörtgen bir yüzey (eğik bir silindirse, o zaman yüzey bükülmüş bir eşkenar dörtgendir).
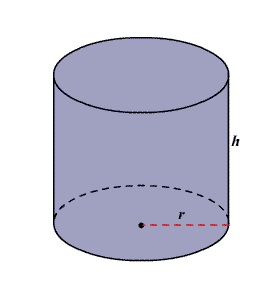
Silindirin Alanı
Bir silindirin alanını hesaplamak için yapısının dikkate alınması gerekir. Yüzeyinin dairesel ve dikdörtgen yüzeyler içermesi nedeniyle, alanını temsil etmek için bu kurucu bileşenlerin alanını hesaplamak için formülleri kullanmamız mantıklıdır.
Bir silindirin alanını hesaplama formülü şöyledir:
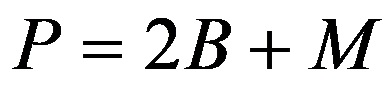
burada 2B dairenin alt ve üstteki alanını, M ise daire çevresinin alanını belirtir.
B’nin dairesel yüzeylerin alanı olduğu göz önüne alındığında, B’nin formüldeki yeri şu şekilde değiştirilebilir:
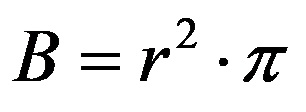
M (dikdörtgen) yerine değiştirildi:
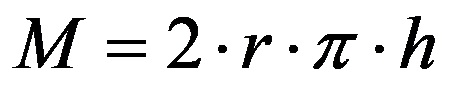
burada h silindirin yüksekliğini temsil eder. Silindirin alanı formülündeki B ve M formüllerini değiştirirsek aşağıdaki formülü elde ederiz:
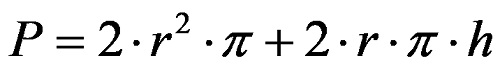
Son denkleme dikkatli bakarsanız hem birinci hem de ikinci toplamın içerdiği üç terim vardır. Bunları parantezlerden önce katları halinde çıkarırsak silindirin alanı formülünün son halini elde ederiz:
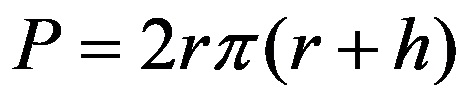
Örnek 1: Taban yarıçapı 2 cm, yüksekliği 10 cm olan bir silindirin alanını hesaplamak.
Alanı hesaplamak için ana formülde verilen değerleri değiştirerek ifade elde edilir:
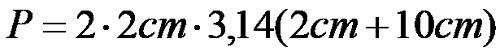
Parantezden önceki ileri çarpımı ve parantez içindeki toplamı gerçekleştirdikten sonra şunu elde ederiz:
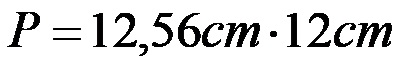
Son ifadedeki sayıların çarpımı hesaplandıktan sonra görev numarası 1’deki silindirin alanının 150,72 santimetrekare olduğu elde edilir.
Aşağıdaki videoda silindirin alan formülünün nasıl oluştuğunu, silindirin yapısını ve bazı alıştırmaları görün.
Silindirin Hakkında Video
Silindirin Hacmi
Silindirin hacmini hesaplama formülü şöyledir:
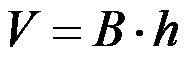
Formülde B yine yukarıdaki metinden bildiğimiz silindir tabanının alanını temsil eder. Tabanın formülünü değiştirerek silindirin hacmine ilişkin formül son değişkeni elde eder:
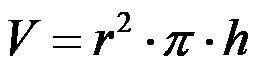
Örnek 2: Taban yarıçapı 2cm, yüksekliği 10cm olan silindirin hacmini hesaplayınız.
Bir silindirin hacmi için son formüldeki problemden verilen değerleri değiştirerek ifade elde edilir:
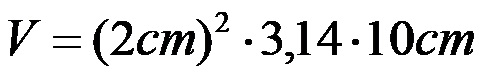
Mezun olduktan sonra nereden şunları alırsınız:
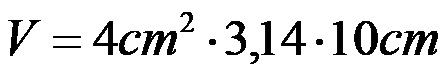
Son ifadedeki üç sayının çarpımı hesaplandıktan sonra 2. problemdeki silindirin hacminin 125,6 santimetreküp olduğu elde edilir.
Aşağıdaki videoda silindirin hacmini hesaplama formülünün nasıl oluştuğunu ve çözülmüş birçok örnek problemi görebilirsiniz.
Ses Seviyesi Videosu
www.mathematikazavsicki.com/tr/’u takip edin!
www.matematikazavsicki.com/tr/’un Facebook, Instagram, Twitter ve Youtube profillerine aşağıdaki butonları kullanarak bağlanarak gelecekte yayınlanacak bilgi ve materyalleri takip edebilirsiniz.