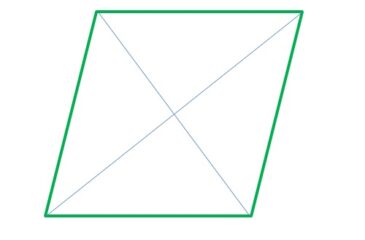
Bir eşkenar dörtgen köşegenler, eşkenar dörtgenin açılarının ortaortaylarıdır. Açıları ikiye bölerler ama diğer yandan karşılıklı olarak birbirlerini ortalarlar. Bunun tam olarak ne anlama geldiğini analiz edelim!
Eşkenar Dörtgen Köşegenler Açıların Ortaortaylarıdır
İki köşegen dört açının tamamını ikiye böler. Önünüzde eşkenar dörtgendeki açılardan birinin (veya tüm açıların) boyutunu belirlemeniz gereken bir göreviniz varsa, bu kural belirli matematik görevlerinde çok yararlı olabilir. Herhangi bir eşkenar dörtgende zıt açıların birbirine eşit olduğunu unutmayalım.
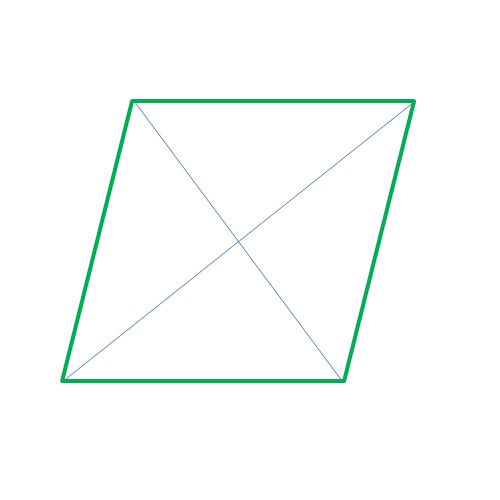
Köşegenler Birbirini Ortalar
Eşkenar dörtgendeki iki köşegen ikiye bölünmüştür, yani tam orta noktalarında kesişirler. Bu herhangi bir eşkenar dörtgen için geçerlidir. Kesin olarak bu bilgiyle geometrik görevlerde çok sayıda problemin çözülebileceği ve bu gerçeğin etkili bir şekilde kullanılabileceği açıktır.
Diğer geometri yasalarıyla, Pisagor teoremi (köşegenlerin çizilmesi eşkenar dörtgende dört dik üçgen üretir) ile birleştirildiğinde, köşegenlerin orta noktada kesiştiği gerçeği birçok sorunu çözmek için çok güçlü bir silahtır.
Bir Eşkenar Dörtgenin Köşegenlerinin Kesişiminde Bir Tepe Noktasına Sahip Olan Açıların Her Biri 90 Derecedir
Mantıksal olarak eşkenar dörtgenin iki köşegeninin kesişimi dört açı oluşturur. Bu dört farklı açının birbirine eşit olduğunu ve her birinin tam olarak 90 derece (dik açı) olduğunu bilmek önemlidir. Bu kesinlikle çok yararlı bir bilgidir çünkü eşkenar dörtgeni dört dik üçgene bölmemiz bize Pisagor teoreminin uygulanmasının elimizde olduğunu ve bunu bilinmeyen boyuttaki açıları veya bilinmeyen uzunluktaki kenarları belirlemek için kullanabileceğimizi söyler.
Rom’daki köşegenlerle ilgili bu üç gerçek çok faydalıdır ve hiç kimse bunları unutmamalıdır. Belirli bir sorunu çözebilmek için mantığı ve daha farklı bilgileri kullanmak zorunda olduğunuz bu matematiksel-geometrik görevlerde, her zaman “kutunun dışında” düşünmeye çalışın. İyi şanlar!
www.mathematikazavsicki.com/tr/’u takip edin!
www.matematikazavsicki.com/tr/’un Facebook, Instagram, Twitter ve Youtube profillerine aşağıdaki butonları kullanarak bağlanarak gelecekte yayınlanacak bilgi ve materyalleri takip edebilirsiniz.
Tags: Dörtgen, Eşkenar, Köşegenler