Bu sayfada daire ve dairenin tanımı, önemli özellikleri ve elemanları, parçaları ve bunların özelliklerini hesaplama formülleri ile ilgili en önemli bilgileri bulabilirsiniz.
Dairesel Çizgi
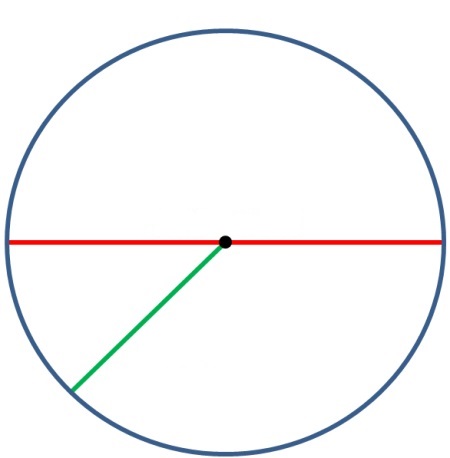
Daire, belirli bir düzlemdeki belirli bir noktadan eşit uzaklıkta bulunan noktaların kümesidir. Bu nokta O ile gösterilir ve çemberin merkezi olarak adlandırılır.
Bir dairenin önemli bölümleri:
- Yarıçap – bir uç noktası dairenin merkezinde ve ikinci uç noktası dairenin üzerinde olan bir doğru parçası.
- Akor – uç noktaları daire üzerinde bulunan bir segment.
- Çap – dairenin merkezinden geçen kiriş.*
Çap, yarıçapın iki katı kadardır!
Bir çevre için önemli kurallar:
- Kesen – daireyi iki noktada kesen çizgi.
- Teğet – daireye yalnızca bir noktada değen bir çizgi.
Bir dairedeki önemli açılar:
- Merkez açı – köşesi dairenin merkezinde olan açı
- Çevresel açı – tepe noktası daire üzerinde bulunan ve bacaklar onunla kesişen bir açı.
Bir Dairenin Çevresi (Daire)
Bir dairenin çevre formülü şu şekildedir:
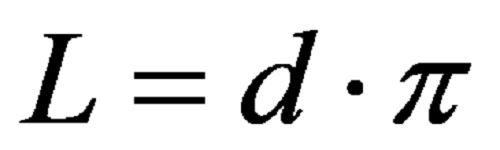
Bir dairenin (dairenin) çevresini hesaplamak için çapı PI sayısıyla çarpmak yeterlidir (sabit – sonsuz sayıda ondalık basamağa sahip bir ondalık sayı). PI numarasının dördüncü ondalık basamağa yuvarlanan değeri 3,1416’dır.
Formülde çapı yarıçapın iki katı olarak değiştirirsek, o zaman bir dairenin (dairenin) çevresi için en sık kullanılan formül elde edilir ve şöyle okunur:
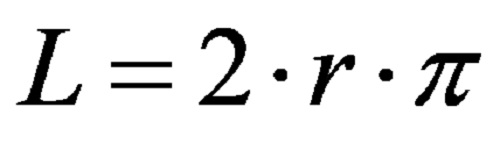
Doğrudan ikinci formülü kullanırsak, yarıçapı biliniyorsa bir dairenin (dairenin) çevresi hesaplanabilir.
Örnek 1: Yarıçapı 10 cm olan bir dairenin çevresini hesaplayın.
- a) Çemberin yarıçapını 2 ile çarpıyoruz.
- b) İlk bölümdeki değeri PI 3.1416 sayısının değeriyle çarpıyoruz.
Örnek 1’deki dairenin (dairenin) çevresi 62.832 santimetredir. **
**PI numarasının dördüncü ondalık basamağına yuvarlanması nedeniyle çevre değeri yaklaşık olarak doğrudur.
Daire
Daire, bir dairenin çevrelediği bir düzlemin kısmını kaplayan 2 boyutlu geometrik bir şekildir.
Bir daire ile bir dairenin tamamen farklı iki şey olduğunu anlamak önemlidir. Daire bir çizgidir, daire ise geometrik bir şekildir.

Bir Dairenin Alanı
Çap cinsinden ifade edilen bir dairenin alanı formülü şöyledir:
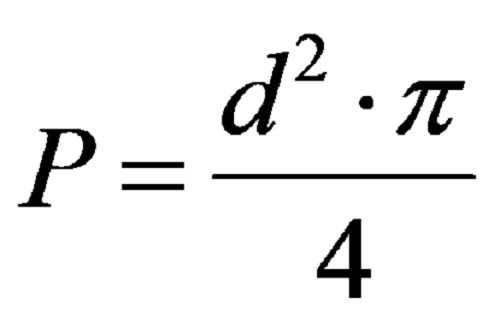
Bununla alanı hesaplamak için çapın karesini sabit PI ile çarpmamız ve ardından bunların çarpımını 4 sayısına bölmemiz gerekir.
Yarıçapı cinsinden ifade edilen bir dairenin alanı formülü daha sık kullanılır. Bu formül şöyle:
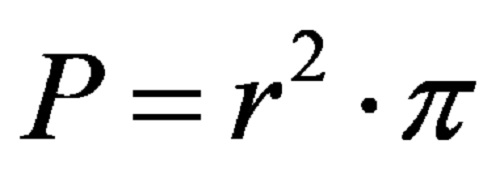
Yine çevre hesaplamasında olduğu gibi, bir dairenin alanını hesaplamak için PI’nin her zaman aynı değer olduğunu akılda tutarak sadece dairenin yarıçapını bilmek yeterlidir.
Örnek 2: Yarıçapı 10 cm olan bir dairenin alanını hesaplayın.
- a) Çemberin yarıçapını 2 oranında ölçeklendiririz.
- b) İlk bölümdeki değeri PI 3.1416 sayısının değeriyle çarpıyoruz.
2 numaralı örnekteki dairenin alanı 314,16 santimetre karedir.
Bir Dairenin Ve Dairenin Bölümleri
Matematikteki birçok hesaplamayla ilgili olan çember ve çember ile ilgili önemli kısımlar şunlardır:
- Dairesel yay – üzerinde bulunan iki noktayla sınırlanan bir dairenin parçası.
- Dairesel parça – daire ve onun yarıçaplarından ikisi tarafından sınırlanan bir dairenin parçası.
- Dairesel parça – daire ve onun kirişlerinden biri tarafından sınırlanan dairenin bir kısmı.
www.mathematikazavsicki.com/tr/’u takip edin!
www.matematikazavsicki.com/tr/’un Facebook, Instagram, Twitter ve Youtube profillerine aşağıdaki butonları kullanarak bağlanarak gelecekte yayınlanacak bilgi ve materyalleri takip edebilirsiniz.
Tags: Akor, Alanı, Çap, Çevre, Çevresel açı, Çizgi, Daire, Dairesel parça, Dairesel yay, Formülü, Kesen, Merkez açı, Teğet, Yarıçap