Bir piramit, bir çokgen olan bir tabana ve tabandaki çokgenin kenar sayısına eşit sayıda yan duvarlara sahip olan geometrik bir gövdedir.
Bir tarafta tüm yan duvarlar tabana tutturulurken, karşı tarafta (eğer piramit tamamlanmışsa) hepsi piramidin tepesi adı verilen aynı noktada bitiyor. Piramidin tepesini tabana dik açıyla bağlayan parçaya piramidin yüksekliği denir ve H (Latince) ile gösterilir.
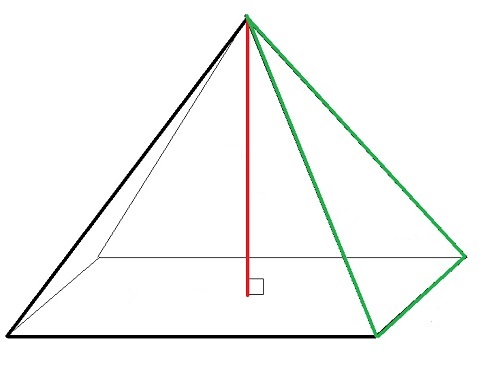
Piramit Türleri
Piramitler iki farklı kritere göre farklı piramit türlerine ayrılabilir:
a) Tabanın geometrik şekline göre piramitler aşağıdakilere ayrılır:
- Üçgen piramit (piramidin tabanı bir üçgen ise)
- Dörtgen piramit (piramidin tabanı dörtgen ise)
- Beşgen piramit (piramidin tabanı beşgen ise)
Mantıksal olarak, tabandaki çokgenin açılarının (kenarlarının) sayısına bağlı olarak buna piramit de denir!
b) Piramidin yüksekliği ile tabanının bulunduğu düzlemin oluşturduğu açının boyutuna göre piramit şöyle olabilir:
Düz – yükseklik ve taban birbirine dik açıdaysa.
Eğik – yükseklik ve taban dik açıdan farklı bir açıyı kapsıyorsa.
Tabanı eşit kenarlı bir çokgen ise ve taban ile yükseklik arasındaki açı dik açı ise, bir piramidin düzenli olduğu söylenebilir. Bu tip piramitlerde tüm yan duvarlar birbirine eşit ikizkenar üçgenlerdir.
Bir Piramidin Alanı
Bir piramidin alanı aşağıdaki formül kullanılarak hesaplanır:
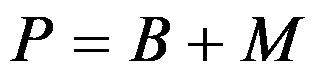
burada B tabanın alanını, M ise yan duvarların toplam alanını gösterir.
Bir piramidin alanını hesaplama formülü, piramidin türüne göre ayarlanmalıdır. Piramit üçgense, piramidin alanını hesaplamak için üçgenin alan formülünü kullanmamız gerekir; tabanın yalnızca bir üçgen olduğunu, M’nin ise üç kenardan oluştuğunu akılda tutarak üçgen şekli.
Eğer piramit saç ise, o zaman hesaplama gerçekten karmaşık hale gelir çünkü tüm yan duvarlar birbirinden farklıdır.
Alan Sorunu
Örnek 1: Kenar uzunluğu 30 cm ise, tabanı 20 cm olan kare tabanlı normal bir piramidin alanını hesaplayın.
Görevi çözme prosedürü aşağıdaki rotayı takip eder:
a) Taban alanının karenin alanı formülüne göre hesaplanması. (M değeri)
b) Heron formülü ile ikizkenar üçgenin alanının hesaplanması (birkaç yolla yapılabilir). Dört eşit kenar olduğundan değer 4 ile çarpılır. (değer B).
c) M için elde edilen değer ile B için elde edilen değerin toplamının hesaplanması.
Çözüm:
a) Piramidin taban alanının hesaplanması:
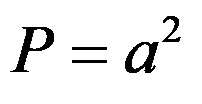
tabanın kenar uzunluğunun değerini değiştirerek şunu elde ederiz:
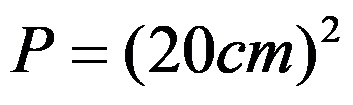
bundan tabanın alanının 400 santimetre kare olduğu anlaşılmaktadır. Bu değer piramidin alanını hesaplamak için kullanılan formülün B değerini temsil eder.
b) Kenarları 20cm, 30cm ve 30cm olan bir üçgen olan piramidin yan duvarı için Heron formülü kullanılarak bir üçgenin alanının 283’e eşit olduğu elde edilir ( yaklaşık) santimetre kare. Formülden M değerinin tamamını elde etmek için bir yan duvarın alanı değeri 4 ile çarpılarak M değeri 1132 santimetrekare elde edilir.
c) Piramidin alanı B ve M’nin toplamı olarak yer değiştirir. Nihai sonuç 1532 santimetre karedir.
Bir Piramidin Hacmi
Bir piramidin hacmi aşağıdaki formül kullanılarak hesaplanır:
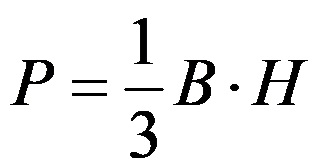
Herhangi bir piramidin hacmini belirlemek için piramidin taban alanı ile piramidin yüksekliğinin çarpımının üçte birini hesaplamamız gerekir.
Örnek 2: Piramidin yüksekliği 25 cm ise, tabanı kare ve kenarı 15 cm olan bir piramidin hacmini hesaplayın.
Görevi çözmek için gereklidir:
a) Tabanın alanını hesaplamak için (kare formülüne göre 225 santimetre kare elde edilir, (bkz. örnek 1).
b) Taban alanı değeri H yüksekliği ile çarpılır. Bu iki değerin çarpımı 5625 santimetreküp olur.
c) Son olarak b) şıkkında elde edilen değerin üçte biri hesaplanır. 5625’in üçte biri 1875’tir.
2 numaralı örnekteki piramidin hacmi 1875 santimetreküptür.
www.mathematikazavsicki.com/tr/’u takip edin!
www.matematikazavsicki.com/tr/’un Facebook, Instagram, Twitter ve Youtube profillerine aşağıdaki butonları kullanarak bağlanarak gelecekte yayınlanacak bilgi ve materyalleri takip edebilirsiniz.