Küp, bitişik kenarlar arasındaki tüm açıların dik (her biri 90 derece) olduğu, altı eşit kare kenara sahip geometrik bir cisimdir. Küpün tüm kenarları birbirine eşittir.
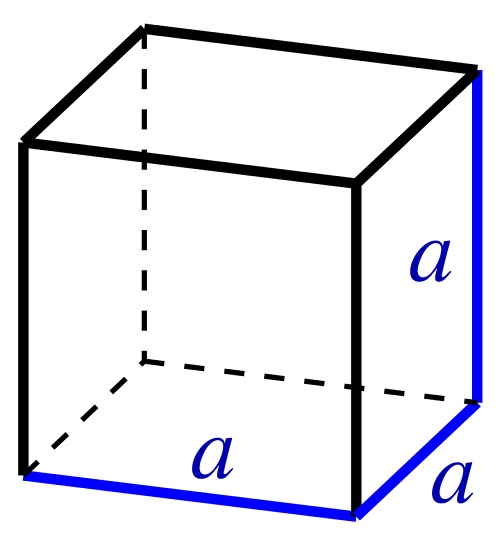
Küpün belirli özelliklerini hesaplamak için gereken tek bilgi kenarının uzunluğudur.
Elementler
Her küpte şunlar bulunur:
- 6 taraf – birbirine eşit.
- 8 köşe – bir köşe, üç farklı tarafın temas ettiği yerdir.
- 12 kenar – birbirine eşit – kenar, iki bitişik kenarın temas ettiği yeri temsil eden bir parçadır.
Küpün Alanı
Bir küpün kenarlarının yalnızca kare olabileceğini bildiğimiz için elbette küpün alanını hesaplamak için bu geometrik şeklin alanını hesaplama formülünü kullanmalıyız.
Elbette küpün 6 kenarı olduğu için hesaplamada hepsinin dikkate alınması gerekir. Bir küpün tüm kenarlarının birbirine eşit olması uygundur, bu nedenle küpün alan formülünde hepsini aynı anda gruplandırabilirsiniz. Bir küpün alanını hesaplama formülü şöyledir:
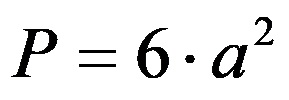
Görev numarası 1: Kenar uzunluğu 8 cm olan bir küpün alanını hesaplayın.
a) Küpün kenarının karesini (derece 2) hesaplıyoruz.
b) a) şıkkında elde ettiğimiz değeri 6 sayısıyla çarpıyoruz.
Prosedür şu şekilde ilerlemelidir:
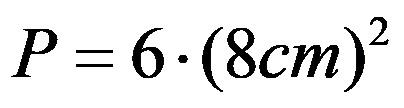
ölçeklendirmenin hesaplanmasından sonra kayıt şu şekli alır:
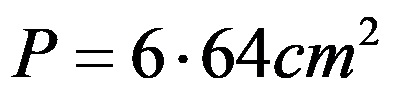
Çarpma işleminden sonra küpün alanı 384 santimetrekare elde edilir.
Bir Küpün Hacmi
Bir küpün hacminin formülü:
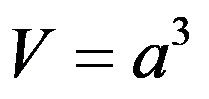
Bir küpün hacmini hesaplamak için kenarının uzunluğunun üçüncü kuvvetini belirlemek yeterlidir.
Görev numarası 2: Kenar uzunluğu 8 cm olan bir küpün hacmini hesaplayın.
Hesaplama basittir ve küpün kenar uzunluğunu kendisiyle üç kez çarpmamızı, yani üçüncü kuvvetini bulmamızı gerektirir.
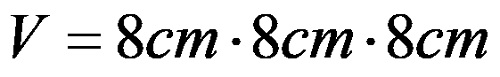
Hesaplamadan küpün hacminin 512 santimetreküp olduğu anlaşılmaktadır.
Bu geometrik katı özel bir tür küboiddir. Küp kelimesinden gelen bağlantıya tıklayarak dikdörtgen prizma alanı ve hacmi ile ilgili problemlerin yer aldığı videonun karşınıza çıktığı sayfaya gidebilirsiniz!
www.mathematikazavsicki.com/tr/’u takip edin!
www.matematikazavsicki.com/tr/’un Facebook, Instagram, Twitter ve Youtube profillerine aşağıdaki butonları kullanarak bağlanarak gelecekte yayınlanacak bilgi ve materyalleri takip edebilirsiniz.