Asal Çarpanlara Ayırma? Asal çarpanların ayrıştırılması, belirli bir karmaşık sayının asal sayı olan faktörlerin çarpımı olarak temsil edildiği bir prosedürdür! Metinde, daha kolay yazma ve okuma için çarpma işaretinin yerini x işareti almıştır!
Hatırlatma olarak:
- Asal sayı, kendisine ve 1 sayısına bölünebilen bir sayıdır. Bir asal sayıyı (1’den ve sayıdan farklı) herhangi bir sayıya böldüğümüzde kalan elde edilir.
- Karmaşık sayı, kendisine ve 1 sayısına bölünebilmesinin yanı sıra en az bir başka sayıya da bölünebilen herhangi bir sayıdır.
Asal Çarpanlara Ayırma Verileri
Aşağıda asal çarpanları çarpanlara ayırmanın üç farklı örneğini çözüm ve açıklamalarla birlikte görebilirsiniz. Bu üç örneğin altında 1’den 100’e kadar olan sayıların asal çarpanlarının ayrıştırılmasını gösteren bir tablonuz var. Tabloda veri olarak 1’den 100’e kadar olan sayı aralığında bulunan tüm asal sayıları görebilirsiniz. Altta Sayfanızda 1’den 100’e kadar tüm sayıların videolu dökümleri mevcut!
Asal çarpanları çarpanlarına ayırma örnekleri
Örnek 1: 14 sayısını asal çarpanlarına ayırın!
14 sayısını 2 ve 7 sayılarının çarpımı olarak gösterebiliriz. Hem 2 hem de 7 sayısı asal sayı olduğu için burada ayrıştırma ilk adım gerçekleştikten hemen sonra bitiyor! Bir çizim üzerinde çözümü şu şekilde sunabiliriz:
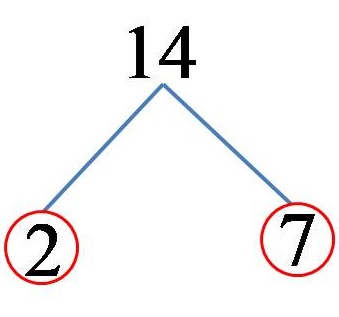
Bundan, 14 sayısının asal katlarına ayrıştırılmasının şu şekilde olduğu anlaşılmaktadır:
14 = 2 x 7
Örnek 2: 30 sayısını asal çarpanlarına ayırın!
30 sayısı, 2 ve 15 sayılarının çarpımı olarak gösterilebilir. 2 sayısı da asal sayı olduğu için 30 sayısının asal çarpanını zaten elde etmiş olduk. Öte yandan 15 sayısı da şu şekilde gösterilebilir: 3 ve 5 sayılarının çarpımı. 3 ve 5 sayıları (her ikisi de) asal sayılardır, bundan sonra 30 sayısının asal katlarının 2, 3 ve 5 sayıları olduğu sonucuna varırız. çözüm şu şekilde:
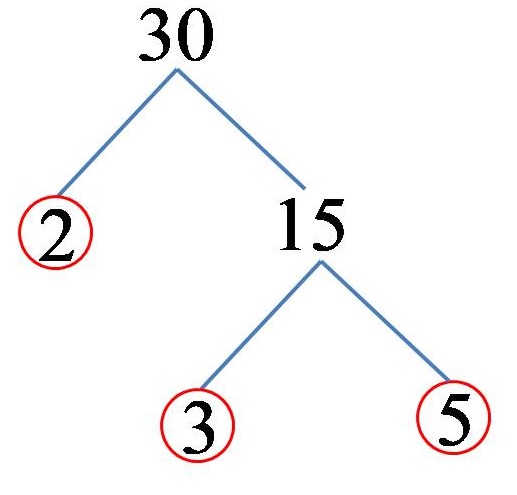
Bundan, 30 sayısının asal katlarına ayrıştırılmasının şu şekilde olduğu anlaşılmaktadır:
30 = 2 x 3 x 5
Örnek 3: 42 sayısını asal çarpanlarına ayırın!
42 sayısını 2 ve 21 sayılarının çarpımı olarak gösterebiliriz. 2 sayısı, 42 sayısının asal katlarından biridir! Öte yandan 21 sayısını 3 ve 7 sayılarının çarpımı olarak da gösterebiliriz. 3 ve 7 sayıları (her ikisi de) asal sayılar olduğundan 42 sayısının asal katlarının 2 olduğu sonucuna varırız. 3 ve 7. Çizimde çözümü şu şekilde gösterebiliriz:
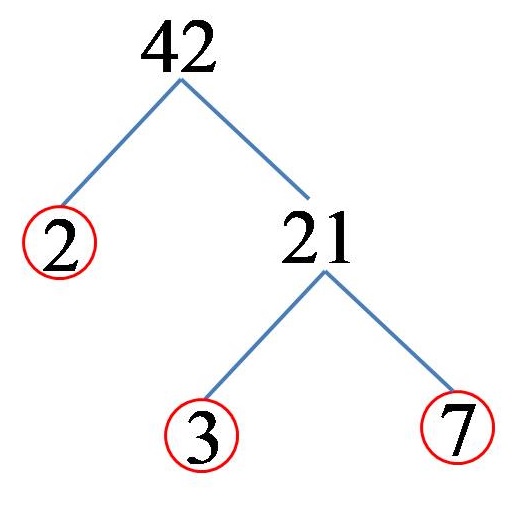
Buradan 42 sayısının asal katlarına ayrıştırıldığı sonucu şu şekilde çıkar:
42 = 2 x 3 x 7
Arıza Tablosu
Aşağıdaki tablo, 1’den 100’e kadar olan tüm sayıların asal çarpanlarına ayrılmasıyla ilgili bilgilerin yanı sıra, 1’den 100’e kadar olan tüm asal sayıların verilerini de içermektedir!
| Sayı | Arıza (mümkünse) |
|---|---|
| 1 | Asal Sayı |
| 2 | Asal Sayı |
| 3 | Asal Sayı |
| 4 | 4 = 2 x 2 |
| 5 | Asal Sayı |
| 6 | 6 = 2 x 3 |
| 7 | Asal Sayı |
| 8 | 8 = 2 x 2 x 2 |
| 9 | 9 = 3 x 3 |
| 10 | 10 = 2 x 5 |
| 11 | Asal Sayı |
| 12 | 12 = 2 x 2 x 3 |
| 13 | Asal Sayı |
| 14 | 14 = 2 x 7 |
| 15 | 15 = 3 x 5 |
| 16 | 16 = 2 x 2 x 2 x 2 |
| 17 | Asal Sayı |
| 18 | 18 = 2 x 3 x 3 |
| 19 | Asal Sayı |
| 20 | 20 = 2 x 2 x 5 |
| 21 | 21 = 3 x 7 |
| 22 | 22 = 2 x 11 |
| 23 | Asal Sayı |
| 24 | 24 = 2 x 2 x 2 x 3 |
| 25 | 25 = 5 x 5 |
| 26 | 26 = 2 x 13 |
| 27 | 27 = 3 x 3 x 3 |
| 28 | 28 = 2 x 2 x 7 |
| 29 | Asal Sayı |
| 30 | 30 = 2 x 3 x 5 |
| 31 | Asal Sayı |
| 32 | 32 = 2 x 2 x 2 x 2 x 2 |
| 33 | 33 = 3 x 11 |
| 34 | 34 = 2 x 17 |
| 35 | 35 = 5 x 7 |
| 36 | 36 = 2 x 2 x 3 x 3 |
| 37 | Asal Sayı |
| 38 | 38 = 2 x 19 |
| 39 | 39 = 3 x 13 |
| 40 | 40 = 2 x 2 x 2 x 5 |
| 41 | Asal Sayı |
| 42 | 42 = 2 x 3 x 7 |
| 43 | Asal Sayı |
| 44 | 44 = 2 x 2 x 11 |
| 45 | 45 = 3 x 3 x 5 |
| 46 | 46 = 2 x 23 |
| 47 | Asal Sayı |
| 48 | 48 = 2 x 2 x 2 x 2 x 3 |
| 49 | 49 = 7 x 7 |
| 50 | 50 = 2 x 5 x 5 |
| 51 | 51 = 3 x 17 |
| 52 | 52 = 2 x 2 x 13 |
| 53 | Asal Sayı |
| 54 | 54 = 2 x 3 x 3 x 3 |
| 55 | 55 = 5 x 11 |
| 56 | 56 = 2 x 2 x 2 x 7 |
| 57 | 57 = 3 x 19 |
| 58 | 58 = 2 x 29 |
| 59 | Asal Sayı |
| 60 | 60 = 2 x 2 x 3 x 5 |
| 61 | Asal Sayı |
| 62 | 62 = 2 x 31 |
| 63 | 63 = 3 x 3 x 7 |
| 64 | 64 = 2 x 2 x 2 x 2 x 2 x 2 |
| 65 | 65 = 5 x 13 |
| 66 | 66 = 2 x 3 x 11 |
| 67 | Asal Sayı |
| 68 | 68 = 2 x 2 x 17 |
| 69 | 69 = 3 x 23 |
| 70 | 70 = 2 x 5 x 7 |
| 71 | Asal Sayı |
| 72 | 72 = 2 x 2 x 2 x 3 x 3 |
| 73 | Asal Sayı |
| 74 | 74 = 2 x 37 |
| 75 | 75 = 3 x 5 x 5 |
| 76 | 76 = 2 x 2 x 19 |
| 77 | 77 = 7 x 11 |
| 78 | 78 = 2 x 3 x 13 |
| 79 | Asal Sayı |
| 80 | 80 = 2 x 2 x 2 x 2 x 5 |
| 81 | 81 = 3 x 3 x 3 x 3 |
| 82 | 82 = 2 x 41 |
| 83 | Asal Sayı |
| 84 | 84 = 2 x 2 x 3 x 7 |
| 85 | 85 = 5 x 17 |
| 86 | 86 = 2 x 43 |
| 87 | 87 = 3 x 29 |
| 88 | 88 = 2 x 2 x 2 x 11 |
| 89 | Asal Sayı |
| 90 | 90 = 2 x 3 x 3 x 5 |
| 91 | 91 = 7 x 13 |
| 92 | 92 = 2 x 2 x 23 |
| 93 | 93 = 3 x 31 |
| 94 | 94 = 2 x 47 |
| 95 | 95 = 5 x 19 |
| 96 | 96 = 2 x 2 x 2 x 2 x 2 x 3 |
| 97 | Asal Sayı |
| 98 | 98 = 2 x 7 x 7 |
| 99 | 99 = 3 x 3 x 11 |
| 100 | 100 = 2 x 2 x 5 x 5 |
| 101 | Asal Sayı |
Video Örnekleri
Video materyalleri, 1’den 100’e kadar tüm sayıların asal çarpanlarını çarpanlara ayırmaya yönelik adım adım bir çözüm içerir:
www.mathematikazavsicki.com/tr/’u takip edin!
www.matematikazavsicki.com/tr/’un Facebook, Instagram, Twitter ve Youtube profillerine aşağıdaki butonları kullanarak bağlanarak gelecekte yayınlanacak bilgi ve materyalleri takip edebilirsiniz.
Tags: Asal, Ayırma, Çarpanlara, Örnek