Pisagor teoremi matematiğin en ünlü teoremlerinden biridir. Bu teorem matematiğin birçok farklı bölümünde ve birçok farklı geometrik problemde geçerlidir. Pisagor teoremi yalnızca dik üçgen için geçerlidir. Pisagor teoreminin tanımı: Bir dik üçgende hipotenüs üzerinde oluşan kare, bu karenin kenarları üzerindeki karelerin alanlarının toplamı ile aynı alana sahiptir.
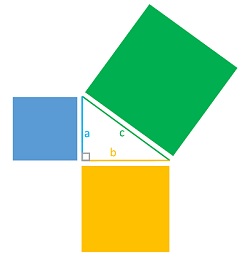
Hipotenüs dik üçgende en uzun kenardır ve her zaman dik açının karşısındadır. Hipotenüs her zaman c harfiyle (küçük Latin harfi c) gösterilir. Dik üçgenin dik açıyı oluşturan diğer iki kenarına bacak denir. Sağ üçgendeki bacaklar a ve b harfleriyle gösterilir (a ve b küçük Latin harfleridir).
Pisagor Teoremi Formülü
Pisagor teoremini temsil eden formül şu şekildedir:
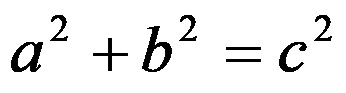
Mantıksal olarak, eğer bir dik üçgenin iki bacağı biliniyorsa, hipotenüs uzunluğu doğrudan belirlenebilir.
Örnek 1: Bir dik üçgenin kenar uzunlukları 9 cm ve 40 cm’dir. Hipotenüs uzunluğunu bulun!
Ana formülde bacaklar için verilen değerlerin değiştirilmesiyle ifade elde edilir:
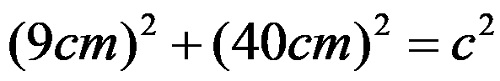
Mezun olduktan sonra nereden şunları alırsınız:
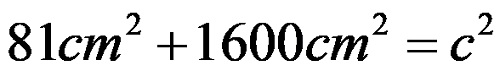
Toplamı oluşturduktan sonra şu elde edilir:
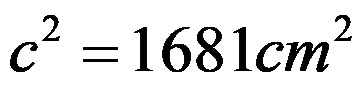
Son ifadeyle hipotenüsün uzunluğunun karesinin ne kadar olduğunu biliyoruz. Hipotenüsün uzunluğunu belirlemek için ifadenin tamamını köklendiriyoruz:
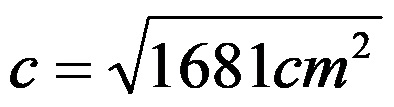
Eşittir işaretinin sağındaki kök hesaplandıktan sonra hipotenüsün uzunluğu 41 cm olur.
Belirli bir problemde bacaklardan biri ve hipotenüs biliniyorsa, bilinmeyen bacak aşağıdaki formüllerden biri kullanılarak belirlenebilir:

Doğru formülün (yukarıdaki iki renkli formülden) kullanılması yalnızca belirli bir durumda hangi bacağın verildiğine ve hangisinin bilinmediğine bağlıdır.
Örnek 2: Bir dik üçgenin hipotenüsünün uzunluğu 25 cm’dir. Bacaklarından birinin uzunluğu 24 cm’dir. Bilinmeyen bacağın uzunluğunu belirleyin!
Anlaşmaya göre bilinen bacağı a harfiyle, bilinmeyen bacağı b harfiyle işaretleyeceğimizi varsayıyoruz. Bu durumda sarı formülü kullanırız. İçinde verilen değerleri değiştirerek ifade elde edilir:
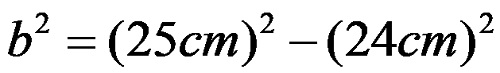
ölçeklendirmeden sonra şu elde edilir:
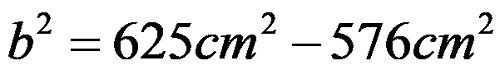
Farkı belirledikten sonra şunu elde ederiz:
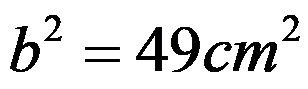
Son ifadeden bilinmeyen bacağın uzunluğunun karesinin ne kadar olduğunu biliyoruz. Uzunluğunu belirlemek için ifadenin tamamını köklendiriyoruz:
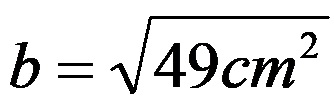
Son olarak köklenme sonrasında bilinmeyen bacağın uzunluğunun 7 cm olduğunu tespit etmek kolaydır.
Başvuru
Aşağıdaki video Pisagor teoreminin doğruluğunun görsel bir kanıtını içermektedir. Ayrıca içinde çözülmüş görevlere ilişkin daha fazla örnek görebilirsiniz.

Pisagor teoremi, bilinmeyen bir hipotenüsün uzunluğunun veya bir dik üçgenin kenarının doğrudan bununla belirlenebildiği durumlarda kullanılır. Elbette matematikte bir dik üçgene geometrik bir cismin parçası, hayali uzay, bir binanın parçası vb. olarak rastlamak mümkündür. Dik üçgenin varlığının belirlenebildiği tüm yerlerde Pisagor teoremi kullanılabilir.
Bu teoremin kullanımı özellikle matematik – trigonometri alanında önemlidir.
Belirli bir dik üçgen için (yukarıdaki çözülmüş problemlerdeki dik üçgenler gibi), kenarlarının uzunluklarının tam sayı olduğu ortaya çıkarsa, bu tür üç sayıya Pisagor üçlüleri denir. İlk çözülmüş örnekten 9, 40 ve 41 sayılarının bir Pisagor üçlüsü olduğu sonucuna varılabilir. İkinci çözülmüş örnekten aynı sonuç 7, 24 ve 25 sayıları için de çıkarılabilir.
Yukarıda sunulan video birkaç Pisagor üçlüsünün bir listesini içerir.
www.mathematikazavsicki.com/tr/’u takip edin!
www.matematikazavsicki.com/tr/’un Facebook, Instagram, Twitter ve Youtube profillerine aşağıdaki butonları kullanarak bağlanarak gelecekte yayınlanacak bilgi ve materyalleri takip edebilirsiniz.
Tags: Pisagor, Pisagor Teoremi, Teoremi