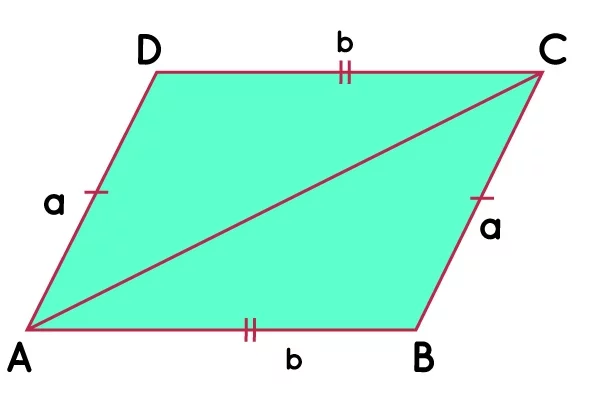
Ромбоид е четириъгълник, който има:
- Две по две успоредни срещуположни страни
- Две по две равни срещуположни страни
- Два по два равни противоположни ъгъла
Ромбоидът се различава от ромба поради дължината на страните му, докато се различава от правоъгълника поради размера на неговите ъгли.
Периметър
Формулата за изчисляване на периметъра на робоид гласи:
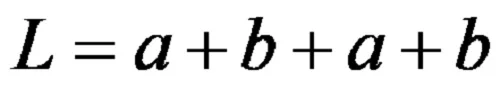
Същата формула, написана с кратни в по-кратка форма, гласи:
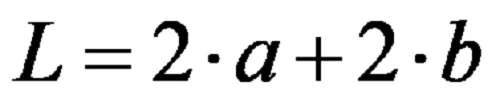
Пример номер едно: Намерете периметъра на ромбоид, ако дължината на по-дългата му страна е 10 cm, а дължината на по-късата му страна е 7 cm.
За решаване на задачата от пример номер едно е достатъчно:
а) Изчислете сумата от дължините на четирите страни. Размерите са: на две места по-дългата страна и на две места по-късата страна: L=10см+7см+10см+7см
б) Да се изчисли сбор от две различни удвоявания на стойностите на по-дългата и по-късата страна на ромбоида.
Периметърът на ромбоида е 16 сантиметра!
Площ на ромбоид
Формулата за изчисляване на площта на ромбоида гласи:

Площта на ромбоида може да се изчисли като произведение на една от страните на ромбоида и съответната му височина.
Пример номер две: Да се изчисли площта на ромбоид със страна 7cm, ако дължината на височината му (съответстваща на дадената страна) е 5cm.
При изчислението е достатъчно да умножите 7 см по 5 см.
Площта на ромбоида от пример номер две е 35 квадратни сантиметра.
Формулите за изчисляване на периметъра и площта на ромбоида са неразделна част от задачите, в които трябва да се изчисляват периметърът и площта на сложни фигури. Също така, формулите се използват като част от задача за изчисляване на площта на определени геометрични тела, които имат страна или повече страни, които имат формата на ромбоид.
Ромбоидът има два диагонала, които не са с еднаква дължина. Двата диагонала се разделят точно наполовина и образуват два равни ъгъла. Тази геометрична фигура няма ос на симетрия.
Последвайте www.mathematikazasite.com/bg!
Следете информацията и материалите, които ще бъдат публикувани в бъдеще, като свържете профилите на www.matematikazavsicki.com във Facebook, Instagram, Twitter и Youtube чрез бутоните по-долу.


 Моля Изчакай...
Моля Изчакай...