Кой метод трябва да се използва за опростяване на дроби до най-простата им форма. По-долу имате правило за опростяване на дроби и два различни подхода за опростяване (съкращаване).
Правило за опростяване на дроби
За да напишем определена дроб в правилна форма (несъкратима дроб), трябва да я преобразуваме в най-простата й форма. За да бъде една дроб в най-простата си форма, нейният числител и знаменател трябва да са две числа, които нямат общ делител, различен от числото 1!
Правилото, което може да ни помогне в една стъпка да извършим необходимото преобразуване в най-простата форма на дробта гласи:
- Първо определяме най-големия общ делител на числителя и знаменателя.
- Разделяме числителя и знаменателя на числото, което е техният най-голям общ делител.
Ако изпълним двете стъпки, описани по-горе, по правилния начин, тогава фракцията, която ще получим след опростяване, е в най-простата си форма.
Пример за използване на правилото
Пример 1: Опростете дадената дроб по-долу до нейната най-проста форма!
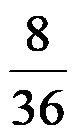
Първи метод! Ако използваме горното правило за опростяване на дроби, следва, че първо трябва да определим най-големия делител на числителя и знаменателя (запомнете как да направите това)!
НОД (8,36) = 4
Най-големият делител (число, на което можем да разделим както числителя, така и знаменателя, което е най-голямото от всички такива възможни числа) за числата 8 и 36 е числото 4. След като разделим числителя и знаменателя, едновременно с числото 4 се получава следният резултат:
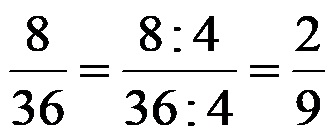
Заключаваме, че дробта 2/9 е най-простата форма на дробта 8/36!
Втори метод! Можем да опростим дробта 8/36 в две стъпки. Ако не искате да търсите най-големия общ делител на числителя и знаменателя, не е нужно. Например, можем да започнем с факта, че 8 и 36 са четни числа. Щом са четни, това означава, че със сигурност се делят на числото 2. Правилно е, ако решим да съкратим дробта 8/36 с числото 2. След като разделим числителя и числителя на числото 2, следният запис за една и съща начална фракция се получава едновременно:
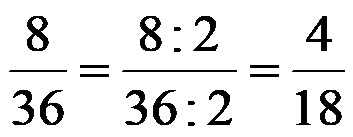
Полученият резултат, т.е. дробта 4/18 е просто още един запис за еквивалентната дроб на дробта 8/36. Този нов запис (тъй като 4 и 18 отново са четни числа), можем допълнително да го разделим на числото 2. Ако извършим това втори път, получаваме следното решение:
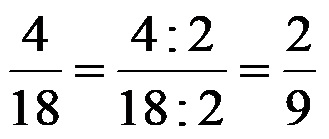
Както може лесно да се види, решението, получено чрез първата методология, и решението, получено чрез втората методология, са еднакви. Това показва, че без значение как опростяваме дроби (независимо дали използваме НОД или не), ако опростим правилно, винаги ще имаме правилното най-просто представяне на дробта, която съкращаваме!
Видео примери
Видеоклипът по-долу съдържа примери за опростяване на дроби до тяхната най-проста форма, като се използва първият метод с най-големия общ делител!
Последвайте www.mathematikazasite.com/bg!
Следете информацията и материалите, които ще бъдат публикувани в бъдеще, като свържете профилите на www.matematikazavsicki.com във Facebook, Instagram, Twitter и Youtube чрез бутоните по-долу.
Tags: Дроби, Опростяване, Правило


 Моля Изчакай...
Моля Изчакай...