Как можете да решите опростяване дроби преди умножение? На тази страница ще видите как да опростите дроби, преди да ги умножите, като по този начин избегнете процедурата по опростяването им след получаване на крайния продукт. Този метод е по-лесен, защото в момента преди умножението е по-лесно да се види кое конкретно число може да бъде опростено, тъй като тук числата, с които работим, са все още относително по-малки.
Опростяване на дроби преди умножение
Когато умножавате две дроби, можете да опростите, както следва:
Намираме числата, които, когато дробите се поставят за умножение, изграждат въображаем “диагонал”. Такива два диагонала се изграждат:
- Числителят на първата дроб и знаменателят на втората дроб
- Знаменателят на първата дроб и знаменателят на втората дроб
По-долу двата различни въображаеми диагонала са маркирани на изображението с различни цветове!
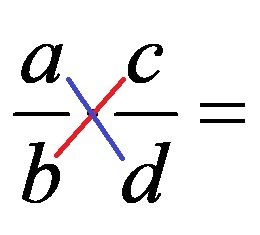
Ако числата, съставляващи диагонала, имат най-голям общ делител, който е различен от 1, тогава разделяме и двете числа на техния НОД и записваме частното на тяхно място. По този начин можем да опростим само един или двата диагонала!
По-долу можете да видите примери, при които опростяването се извършва, преди да умножим дробите!
Примери
Първият пример по-долу съдържа опростяване, което е възможно само по един диагонал, докато вторият пример може да бъде опростен и по двата диагонала!
Пример 1: Опростете дадените по-долу дроби, преди да извършите умножението!
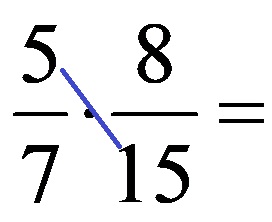
НОД за числата, разположени в маркирания диагонал (числа 5 и 15) е числото 5! Затова разделяме и двете числа на числото 5. Опростяването трябва да изглежда така:
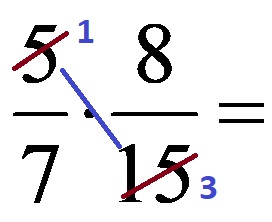
Ако напишем последния израз без коригирани числа, той изглежда така:
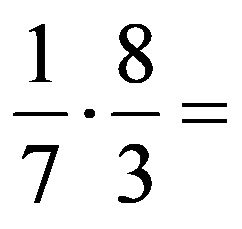
Накрая остава да умножим дробите, което дава следния краен резултат:
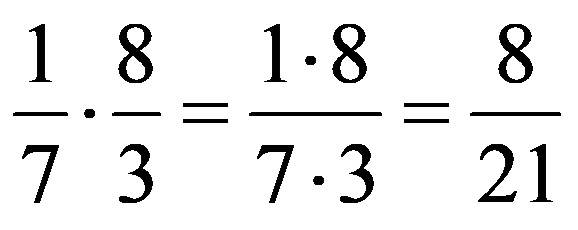
Пример 2: Опростете дроби, преди да ги умножите!
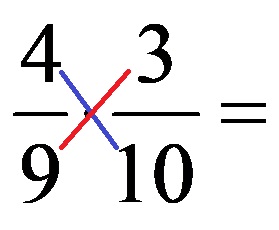
НОД за числата в синия диагонал (числа 4 и 10) е числото 2! Ето защо разделяме и двете числа на числото 2. От друга страна, НОД за числата, които са в червения диагонал (числата 9 и 3) е числото 3. Разделяме двете числа от червения диагонал на числото 3! След опростяване се получава следният израз:
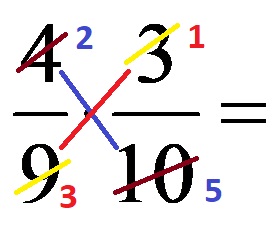
Ако напишем последния израз без коригирани числа, той изглежда така:
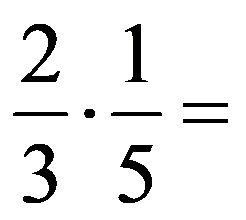
Накрая остава да умножим дробите, което дава следния краен резултат:
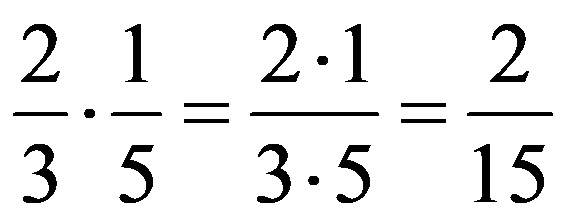
Видео примери
Във видеото по-долу можете да видите много примери за опростяване на дроби, преди да ги умножите!
Ако, когато умножавате дроби помежду си, решите да не се упражнявате да ги опростявате, преди да ги умножите, тогава в крайна сметка (когато получите техния продукт), трябва да опростите крайния резултат, който най-вероятно ще бъде под формата на дроб!
Последвайте www.mathematikazasite.com/bg!
Следете информацията и материалите, които ще бъдат публикувани в бъдеще, като свържете профилите на www.matematikazavsicki.com във Facebook, Instagram, Twitter и Youtube чрез бутоните по-долу.
Tags: Дроби, Опростяване, Преди, Умножение


 Моля Изчакай...
Моля Изчакай...