За да се изчисли общото електрическо съпротивление в комбинирана верига, трябва да се знаят формулите за изчисляване на общото електрическо съпротивление, индивидуално за:
- Серийна верига
- Верига с паралелен ток
Чрез прилагане на формулите за изчисляване на общо електрическо съпротивление в последователна и паралелна токова верига се формира нова формула за комбинирана токова верига, която е валидна само за токовата верига, чието общо съпротивление се определя. Следователно комбинираните вериги са по-сложни за определяне на еквивалентното съпротивление. Примерите, които можете да видите по-долу (в текстов и видео формат), ще ви помогнат да разберете как се образуват нови формули (на базата на тези за последователни и паралелни вериги).
Изчисляване на електрическо съпротивление в комбинирана верига
Схема, която съдържа едновременно последователна и паралелна връзка между консуматори (резистори), се нарича комбинирана верига. Поради комбинацията от последователно и паралелно свързване, при изчисляване на общото съпротивление трябва да се използват индивидуалните формули за двата метода на свързване.
Най-добре е първо да разберете колко различни членове са свързани последователно. Представяме общия резистор в комбинирана верига като сбор от отделните части, свързани последователно.
Разбира се, трябва да се внимава много, тъй като един член, свързан последователно с останалите, може сам да бъде паралелна връзка на два, три или повече члена. В този случай първо се изчислява съпротивлението за този елемент (като се използва формулата за общо съпротивление в паралелни токови вериги) и едва след това с тази стойност се пристъпва към изчисляването на общото съпротивление в комбинираната токова верига.
Най-сложни за решаване са схеми, които имат член, който сам по себе си съдържа както последователна, така и паралелна връзка.
Вижте решения пример по-долу. Този пример съдържа най-простата комбинирана схема с три консуматора (резистори).
Пример за изчисляване на общото съпротивление в комбинирана верига
Пример 1: Изчислете общото (еквивалентно) електрическо съпротивление в комбинираната верига, дадена на фигурата по-долу:
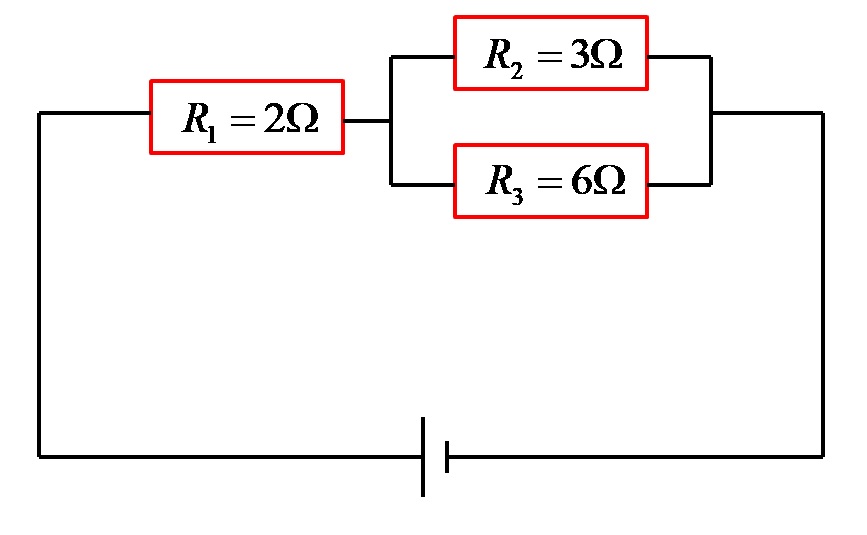
Изображението по-горе съдържа три консуматора, свързани заедно. От снимката става ясно, че токовата верига съдържа две различни части, които са свързани последователно! Това е всичко:
- Първият консуматор с електрическо съпротивление R един.
- Паралелното свързване между втория и третия консуматор с електрическо съпротивление R две и R три съответно.
В тази ситуация, тъй като има само два последователни елемента, за общото съпротивление в комбинираната верига създаваме формулата:
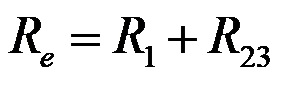
Логично, първо ще определим общото електрическо съпротивление в паралелната връзка R (едно-две), след което с тази стойност ще се върнем към оригиналната формула, за да определим общото електрическо съпротивление за цялата комбинирана верига!
За паралелно свързване използваме формулата с реципрочни стойности, съобразени с броя на консуматорите в конкретния паралелен клон. Той гласи:
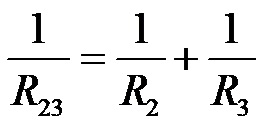
Чрез заместване на стойностите за втория и третия потребител се получава изразът:
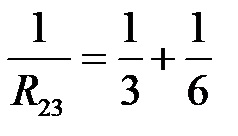
След като заместим НОЗ (най-малкия общ знаменател) за числата 3 и 6 и разширим дробите до знаменателя 6, получаваме:
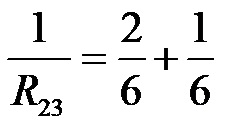
Откъдето, като съберем дробите с еднакви знаменатели, стигаме до последната стъпка:
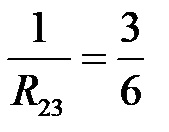
Накрая с подходящо завъртане (отляво и отдясно на знака за равенство) получаваме:
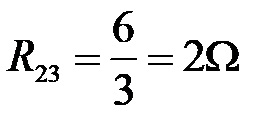
Общото съпротивление на паралелната връзка между втория и третия консуматор е 2 ома.
Накрая остава да заменим предварително получената стойност в първоначалната формула, което ни дава:
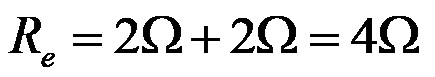
Общото електрическо съпротивление за цялата комбинирана верига е 4 ома!
Видео примери
Видео материалът по-долу съдържа три различни комбинирани схеми, които се получават чрез комбиниране на местоположението на всеки резистор поотделно. В него ще видите следните комбинации:
- Първият консуматор е последователно свързан с паралелното свързване на втория и третия.
- Вторият консуматор е последователно свързан с паралелното свързване на първия и втория.
- Третият консуматор е последователно свързан с паралелното свързване на първия и втория.
Всяка различна комбинирана токова верига е ново условие, което трябва да се анализира добре, да се разбере начина на свързване между различните части и едва след това да се създаде нова формула, която да важи само за тази комбинирана токова верига!
Последвайте www.mathematikazasite.com/bg!
Следете информацията и материалите, които ще бъдат публикувани в бъдеще, като свържете профилите на www.matematikazavsicki.com във Facebook, Instagram, Twitter и Youtube чрез бутоните по-долу.
Tags: Верига, Комбинирана, Общo, Пример, Съпротивление, Формула


 Моля Изчакай...
Моля Изчакай...