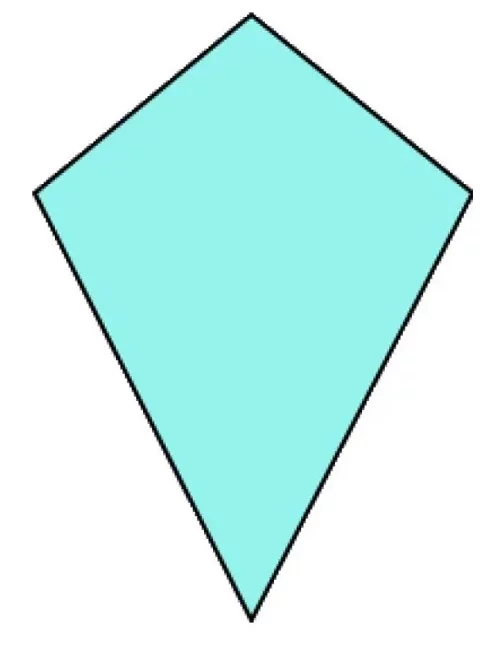
Делтоид е четириъгълник без успоредни страни, който има две съседни равни страни. Може да се каже, че делтоидът е напълно определен, ако са известни дължините на неговите неравни страни и ъгълът между тях.
Периметър
Формулата за периметъра на делтоида гласи:
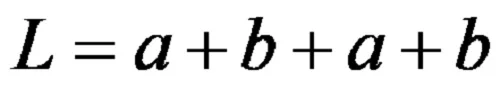
Същата формула, написана с кратни в по-кратка форма, гласи:
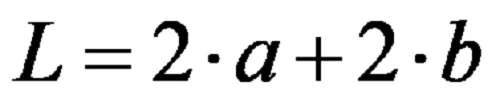
Пример номер 1. Изчислете периметъра на делтоид, ако дължината на по-дългата му страна е 15 cm, а дължината на по-късата му страна е 11 cm.
За решаване на задачата от пример номер едно е достатъчно:
а) Изчислете сумата от дължините на четирите страни. Размерите са: на две места по-дългата страна и на две места по-късата страна: L=15см+11см+15см+11см
б) Да се изчисли сума от две различни удвоявания на стойностите на по-дългата и по-късата страна на делтоида.
Периметърът на делтоида е 52 сантиметра!
Площ на делтоид
Площта на делтоида може да се изчисли с помощта на хероновата формула, както при всеки друг четириъгълник без успоредни страни (вижте примерна решена задача, като щракнете върху връзката). Единствената разлика е, че площта на тази 2D фигура с формулата на Херон, където е известен по-дългият диагонал, е по-лесна за изчисляване, защото в тази ситуация делтоидът е съставен от два еднакви триъгълника.
В допълнение към метода на стандартното решение, площта на делтоида може да се изчисли по формулата:
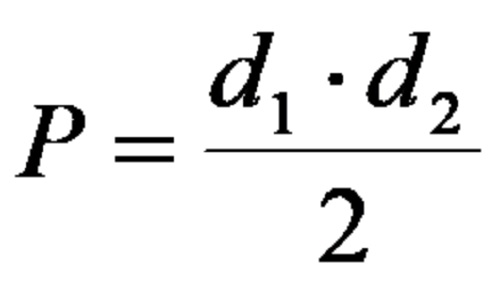
Разбира се, за да използваме формулата директно, трябва да се знае дължината на двата диагонала на делтоида. Ако дължината им е известна, лесно може да се определи площта.
Пример номер 2: Изчислете площта на делтоид, ако са известни дължините на неговите диагонали, които са 3 cm и 16 cm.
За да определите площта, е достатъчно:
- Да се определи произведението на диагоналите.
- Разделете произведението на диагоналите на 2.
Площта на делтоида от пример номер две е 24 квадратни сантиметра.
Диагоналите на делтоида винаги имат различна дължина. Те се пресичат под прав ъгъл (ъгъл от 90 градуса). Делтоидът има една ос на симетрия.
Последвайте www.mathematikazasite.com/bg!
Следете информацията и материалите, които ще бъдат публикувани в бъдеще, като свържете профилите на www.matematikazavsicki.com във Facebook, Instagram, Twitter и Youtube чрез бутоните по-долу.

 Моля Изчакай...
Моля Изчакай...