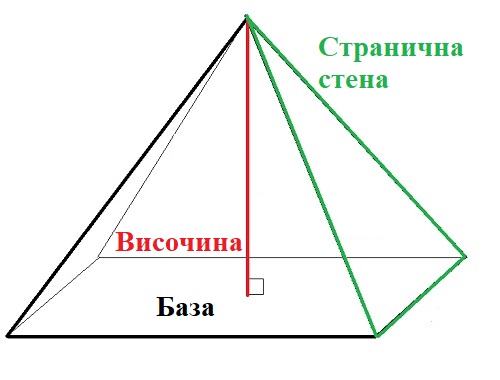
Пирамида е геометрично тяло, което има основа, която е многоъгълник и странични стени с число, равно на броя на страните на многоъгълника в основата.
От една страна, всички странични стени са прикрепени към основата, докато от противоположната страна (ако пирамидата е пълна) всички те завършват в една и съща точка, която се нарича върха на пирамидата. Отсечката, която свързва върха на пирамидата с основата под прав ъгъл, се нарича височина на пирамидата и се обозначава с Н (лат.).
Видове пирамиди
Пирамидите могат да бъдат разделени на различни видове пирамиди според два различни критерия:
a) Според геометричната форма на основата пирамидите се делят на:
- Триъгълна пирамида (ако основата на пирамидата е триъгълник)
- Четириъгълна пирамида (ако основата на пирамидата е четириъгълник)
- Петоъгълна пирамида (ако основата на пирамидата е петоъгълник)
Логично следва, че в зависимост от броя на ъглите (страните) на многоъгълника в основата, той се нарича още пирамида!
b) Според големината на ъгъла, образуван от височината на пирамидата и равнината, в която лежи нейната основа, пирамидата може да бъде:
- Плосък – ако височината и основата са под прав ъгъл една спрямо друга.
- Наклонен – ако височината и основата заемат ъгъл, различен от прав ъгъл.
Може да се каже, че пирамидата е правилна, ако основата й е многоъгълник с равни страни, а ъгълът между основата и височината е прав ъгъл. При този тип пирамиди всички странични стени са равнобедрени триъгълници, които са равни една на друга.
Площ на пирамида
Площта на пирамидата се изчислява по формулата:
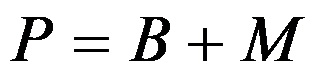
където B показва площта на основата, докато M показва общата площ на страничните стени.
Формулата за изчисляване на площта на пирамидата трябва да бъде съобразена с вида на самата пирамида. Ако пирамидата е триъгълна, тогава за да изчислим площта на пирамидата, трябва да използваме формулата за площта на триъгълник, като имаме предвид, че основата е само един триъгълник, докато M се образува от три страни в формата на триъгълник.
Ако пирамидата е коса, тогава изчислението става наистина сложно, защото всички странични стени са различни една от друга.
Задача с площ
Пример номер 1: Изчислете площта на правилна пирамида, която има квадратна основа със страна 20 cm, ако дължината на страничния й ръб е 30 cm.
Процедурата за решаване на задачата е следната:
a) Изчисляване на площта на основата по формулата за площта на квадрата. (М стойност)
b) Изчисляване на площта на равнобедрен триъгълник (може да се направи по няколко начина) с формулата на Heron. Стойността се умножава по 4, защото има четири равни страни. (стойност B).
c) Изчисляване на сумата от стойността, получена за М, и стойността, получена за В.
Решение:
a) Изчисляване на площта на основата на пирамидата:
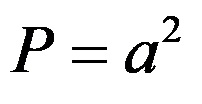
като заместим стойността на дължината на страната на основата, получаваме:
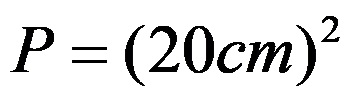
от което следва, че площта на основата е 400 квадратни сантиметра. Тази стойност представлява стойността B на формулата за изчисляване на площта на пирамидата.
b) Използвайки хероновата формула (щракнете тук, за да видите изчисление с формулата на Херон) за страничната стена на пирамидата, която е триъгълник със страни 20 cm, 30 cm и 30 cm, за един триъгълник се получава, че има площ, равна на 283 ( приблизително) квадратни сантиметра. За да получите цялата M стойност от формулата, стойността за площта на едната странична стена се умножава по 4, давайки M стойност 1132 квадратни сантиметра.
c) Площта на пирамидата се транспонира като сбор от B и M. Крайният резултат е 1532 квадратни сантиметра.
Обем на пирамида
Обемът на пирамидата се изчислява по формулата:
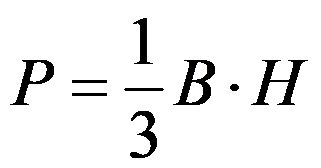
За да определим обема на всяка пирамида, трябва да изчислим една трета от произведението на площта на основата на пирамидата и височината на пирамидата.
Пример номер 2: Изчислете обема на пирамида с квадратна основа и страна 15 cm, ако височината на пирамидата е 25 cm.
За решаване на задачата е необходимо:
a) За изчисляване на площта на основата (според квадратната формула се получават 225 квадратни сантиметра (виж пример номер 1).
b) Стойността за площта на основата се умножава по височината H. Продуктът от тези две стойности е 5625 кубични сантиметра.
c) Накрая се изчислява една трета от стойността, получена в b). Една трета от 5625 е 1875.
Обемът на пирамидата от пример номер 2 е 1875 кубични сантиметра.
Последвайте www.mathematikazasite.com/bg!
Следете информацията и материалите, които ще бъдат публикувани в бъдеще, като свържете профилите на www.matematikazavsicki.com във Facebook, Instagram, Twitter и Youtube чрез бутоните по-долу.


 Моля Изчакай...
Моля Изчакай...