Разлагане на прости множители е процедура, при която определено комплексно число се представя като произведение на множители, които са прости числа!
Напомняне:
- Просто число е число, което се дели на себе си и на числото 1. При деление на просто число на всяко друго число (различно от 1 и от самото число) се получава остатък.
- Комплексно число е всяко число, което освен че се дели на себе си и на числото 1, се дели на поне още едно число.
Данни за разлагане на прости множители
По-долу можете да видите три различни примера за разлагане на прости множители с решение и обяснение. Под тези три примера имате таблица, която представя разлагането на простите множители за числата от 1 до 100. В таблицата като данни можете да видите всички прости числа, които съществуват в диапазона от числа от 1 до 100. В долната част на страницата ви видео разбивки на всички числа от 1 до 100 са налични!
Примери за разлагане на прости множители
Пример 1: Разбийте числото 14 на прости множители!
Можем да представим числото 14 като произведение на числата 2 и 7. Тъй като и числото 2, и числото 7 са прости числа, тук разлагането приключва веднага след реализирането на първата стъпка! На чертеж можем да представим решението по следния начин:
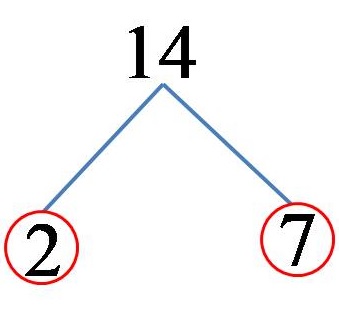
От което следва, че числото 14, разложено на неговите прости кратни, изглежда така:
14 = 2 x 7
Пример 2: Разбийте числото 30 на прости множители!
Числото 30 може да бъде представено като произведение на числата 2 и 15. Тъй като числото 2 също е просто число, вече сме получили прост множител за числото 30. От друга страна, числото 15 може да бъде представено като произведението на числата 3 и 5. Числата 3 и 5 (и двете) са прости числа, след което заключаваме, че простите кратни на числото 30 са числата 2, 3 и 5. На чертеж можем да представим решение по този начин:
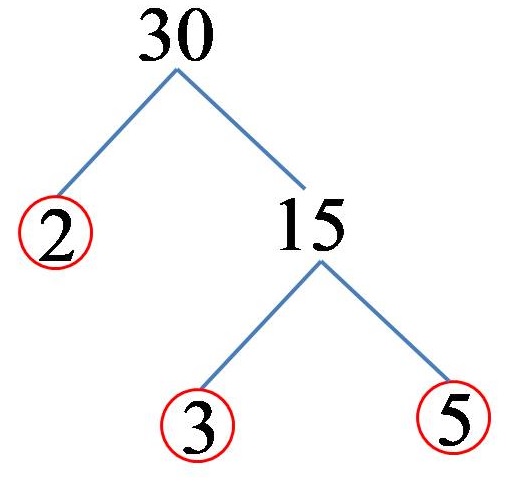
От което следва, че числото 30, разложено на неговите прости кратни, изглежда така:
30 = 2 x 3 x 5
Пример 3: Разбийте числото 42 на прости множители!
Можем да представим числото 42 като произведение на числата 2 и 21. Числото 2 е едно от простите кратни на числото 42! От друга страна, можем да представим числото 21 като произведение на числата 3 и 7. Числата 3 и 7 (и двете) са прости числа, след което заключаваме, че простите кратни на числото 42 са числата 2, 3 и 7. На чертежа решението можем да го представим по следния начин:
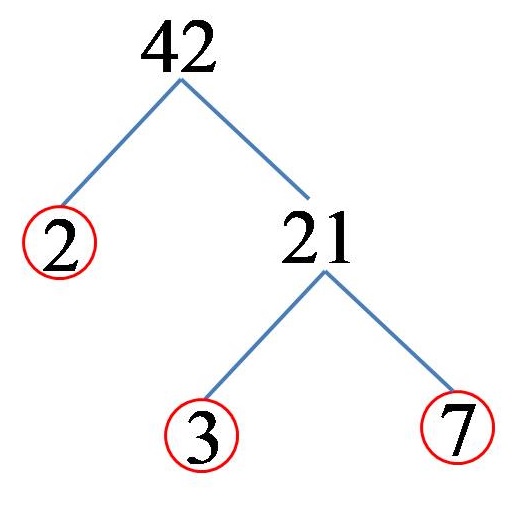
От което следва, че числото 42, разложено на неговите прости кратни, изглежда така:
42 = 2 x 3 x 7
Табела за разложуване
Таблицата по-долу съдържа информация за разлагането на прости числа на всички числа от 1 до 100, както и данни за всички прости числа, които съществуват от 1 до 100!
| Номер | Ралагане (ако е възможно) |
|---|---|
| 1 | Просто число |
| 2 | Просто число |
| 3 | Просто число |
| 4 | 4 = 2 x 2 |
| 5 | Просто число |
| 6 | 6 = 2 x 3 |
| 7 | Просто число |
| 8 | 8 = 2 x 2 x 2 |
| 9 | 9 = 3 x 3 |
| 10 | 10 = 2 x 5 |
| 11 | Просто число |
| 12 | 12 = 2 x 2 x 3 |
| 13 | Просто число |
| 14 | 14 = 2 x 7 |
| 15 | 15 = 3 x 5 |
| 16 | 16 = 2 x 2 x 2 x 2 |
| 17 | Просто число |
| 18 | 18 = 2 x 3 x 3 |
| 19 | Просто число |
| 20 | 20 = 2 x 2 x 5 |
| 21 | 21 = 3 x 7 |
| 22 | 22 = 2 x 11 |
| 23 | Просто число |
| 24 | 24 = 2 x 2 x 2 x 3 |
| 25 | 25 = 5 x 5 |
| 26 | 26 = 2 x 13 |
| 27 | 27 = 3 x 3 x 3 |
| 28 | 28 = 2 x 2 x 7 |
| 29 | Просто число |
| 30 | 30 = 2 x 3 x 5 |
| 31 | Просто число |
| 32 | 32 = 2 x 2 x 2 x 2 x 2 |
| 33 | 33 = 3 x 11 |
| 34 | 34 = 2 x 17 |
| 35 | 35 = 5 x 7 |
| 36 | 36 = 2 x 2 x 3 x 3 |
| 37 | Просто число |
| 38 | 38 = 2 x 19 |
| 39 | 39 = 3 x 13 |
| 40 | 40 = 2 x 2 x 2 x 5 |
| 41 | Просто число |
| 42 | 42 = 2 x 3 x 7 |
| 43 | Просто число |
| 44 | 44 = 2 x 2 x 11 |
| 45 | 45 = 3 x 3 x 5 |
| 46 | 46 = 2 x 23 |
| 47 | Просто число |
| 48 | 48 = 2 x 2 x 2 x 2 x 3 |
| 49 | 49 = 7 x 7 |
| 50 | 50 = 2 x 5 x 5 |
| 51 | 51 = 3 x 17 |
| 52 | 52 = 2 x 2 x 13 |
| 53 | Просто число |
| 54 | 54 = 2 x 3 x 3 x 3 |
| 55 | 55 = 5 x 11 |
| 56 | 56 = 2 x 2 x 2 x 7 |
| 57 | 57 = 3 x 19 |
| 58 | 58 = 2 x 29 |
| 59 | Просто число |
| 60 | 60 = 2 x 2 x 3 x 5 |
| 61 | Просто число |
| 62 | 62 = 2 x 31 |
| 63 | 63 = 3 x 3 x 7 |
| 64 | 64 = 2 x 2 x 2 x 2 x 2 x 2 |
| 65 | 65 = 5 x 13 |
| 66 | 66 = 2 x 3 x 11 |
| 67 | Просто число |
| 68 | 68 = 2 x 2 x 17 |
| 69 | 69 = 3 x 23 |
| 70 | 70 = 2 x 5 x 7 |
| 71 | Просто число |
| 72 | 72 = 2 x 2 x 2 x 3 x 3 |
| 73 | Просто число |
| 74 | 74 = 2 x 37 |
| 75 | 75 = 3 x 5 x 5 |
| 76 | 76 = 2 x 2 x 19 |
| 77 | 77 = 7 x 11 |
| 78 | 78 = 2 x 3 x 13 |
| 79 | Просто число |
| 80 | 80 = 2 x 2 x 2 x 2 x 5 |
| 81 | 81 = 3 x 3 x 3 x 3 |
| 82 | 82 = 2 x 41 |
| 83 | Просто число |
| 84 | 84 = 2 x 2 x 3 x 7 |
| 85 | 85 = 5 x 17 |
| 86 | 86 = 2 x 43 |
| 87 | 87 = 3 x 29 |
| 88 | 88 = 2 x 2 x 2 x 11 |
| 89 | Просто число |
| 90 | 90 = 2 x 3 x 3 x 5 |
| 91 | 91 = 7 x 13 |
| 92 | 92 = 2 x 2 x 23 |
| 93 | 93 = 3 x 31 |
| 94 | 94 = 2 x 47 |
| 95 | 95 = 5 x 19 |
| 96 | 96 = 2 x 2 x 2 x 2 x 2 x 3 |
| 97 | Просто число |
| 98 | 98 = 2 x 7 x 7 |
| 99 | 99 = 3 x 3 x 11 |
| 100 | 100 = 2 x 2 x 5 x 5 |
| 101 | Прост број |
Видео примери
Видео материалите съдържат стъпка по стъпка решение за разлагане на прости множители на всички числа от 1 до 100:
Последвайте www.mathematikazasite.com/bg!
Следете информацията и материалите, които ще бъдат публикувани в бъдеще, като свържете профилите на www.matematikazavsicki.com във Facebook, Instagram, Twitter и Youtube чрез бутоните по-долу.
Tags: Комплексни, Множители, Прости, Разлагане, Числа, Число


 Моля Изчакай...
Моля Изчакай...