Питагорова теорема е една от най-известните теореми в математиката. Тази теорема се прилага в много различни части на математиката и много различни геометрични проблеми. Питагоровата теорема е валидна само за правоъгълен триъгълник. Дефиниция на Питагоровата теорема: В правоъгълен триъгълник квадратът, образуван върху хипотенузата, има същата площ като сумата от площите на квадратите върху неговите катети.
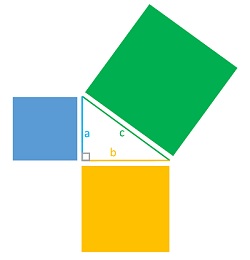
Хипотенузата е най-дългата страна в правоъгълен триъгълник и винаги е срещу правия ъгъл. Хипотенузата винаги се означава с буквата c (малка латинска буква c). Другите две страни на правоъгълен триъгълник, които образуват прав ъгъл, се наричат катети. Краката в правоъгълния триъгълник се означават с буквите a и b (a и b са малки латински букви).
Формула на Питагоровата теорема
Формулата, която представя самата Питагорова теорема гласи:
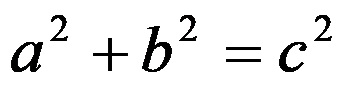
Логично, ако са известни двата катета на правоъгълен триъгълник, тогава дължината на неговата хипотенуза може да се определи директно.
Пример номер 1: Правоъгълен триъгълник има страни с дължина 9 cm и 40 cm. Намерете дължината на неговата хипотенуза!
Чрез заместване на дадените стойности за краката в основната формула се получава изразът:
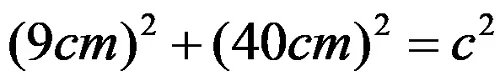
откъдето след степенуването получавате:
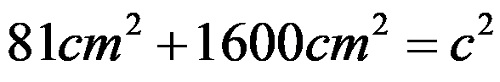
След образуване на сумата се получава, че:
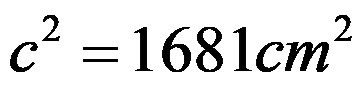
С последния израз знаем колко е квадратът на дължината на хипотенузата. За да определим дължината на хипотенузата, изкореняваме целия израз:
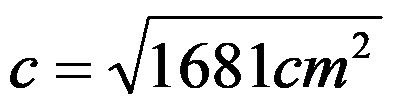
След изчисляване на корена вдясно от знака за равенство се получава стойността 41cm за дължината на хипотенузата.
Ако в дадена задача един от краката и хипотенузата са известни, тогава неизвестният крак може да се определи с помощта на една от формулите:

Използването на правилната формула (от двете оцветени формули по-горе) зависи само от това кой от краката е даден в конкретния случай и кой е неизвестното.
Пример номер 2: Правоъгълен триъгълник има хипотенуза с дължина 25 cm. Единият му крак е с дължина 24 см. Определете дължината на неизвестния крак!
По споразумение приемаме, че ще маркираме познатия крак с буквата a, а непознатия крак с буквата b. В тази ситуация използваме жълтата формула. Чрез заместване на дадените стойности в него се получава изразът:
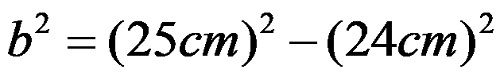
от което след степенуването се получава, че:
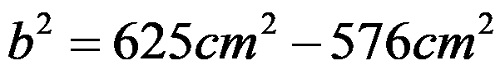
След като определим разликата, получаваме:
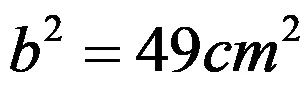
От последния израз знаем колко е на квадрат дължината на неизвестния катет. За да определим неговата дължина, изкореняваме целия израз:
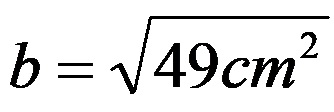
И накрая, след вкореняване е лесно да се определи, че дължината на неизвестния крак е 7 см.
Приложение
Видеото по-долу съдържа визуално доказателство за правилността на Питагоровата теорема. Освен това в него можете да видите още примери за решени задачи.

Питагоровата теорема се използва винаги, когато с нея може директно да се определи дължината на неизвестна хипотенуза или катет на правоъгълен триъгълник. Разбира се, в математиката правоъгълният триъгълник може да се срещне като част от геометрично тяло, въображаемо пространство, част от сграда и т.н. Във всички онези места, където може да се установи съществуването на правоъгълен триъгълник, може да се използва Питагоровата теорема.
Използването на тази теорема е особено важно в частта от математиката – тригонометрията.
Ако за даден правоъгълен триъгълник (като правоъгълните триъгълници от решените задачи по-горе) се окаже, че дължините на страните му са цели числа, то такива три числа се наричат Питагорови тройки. От първия решен пример може да се заключи, че числата 9, 40 и 41 са питагорова тройка. От втория решен пример същото може да се заключи и за числата 7, 24 и 25.
Видеото, представено по-горе, съдържа списък от няколко питагорови тройки.
Последвайте www.mathematikazasite.com/bg!
Следете информацията и материалите, които ще бъдат публикувани в бъдеще, като свържете профилите на www.matematikazavsicki.com във Facebook, Instagram, Twitter и Youtube чрез бутоните по-долу.
Tags: Задачи, Питагорова, Питагорова теорема, Порязвания, Правоъгълен, Теорема, Формула, Хипотенуза


 Моля Изчакай...
Моля Изчакай...